Una de ingenieros.
Elegancia profesional...
Cualquier Ingeniero aprende, desde la infancia, la notación matemática según la cual la suma de dos números reales, como por ejemplo:
1 + 1 = 2
puede ser escrita de manera muy simple. Sin embargo, podemos decir, que está totalmente carente de estilo, sobre todo para un ingeniero.
Desde las primeras clases de Matemáticas sabemos que:
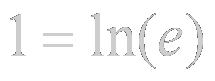
y también que:
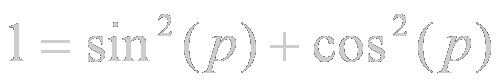
Además, todos saben que:
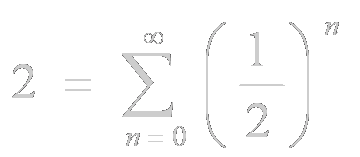
Por lo tanto la expresión
1 + 1 = 2
puede ser reescrita de una forma más elegante así:
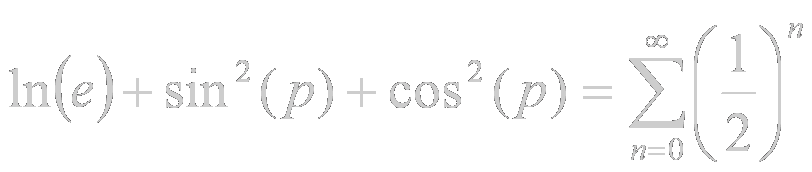
la cual, como fácilmente pueden observar, es mucho más comprensible y científica.
Por otra parte, sabido es que:
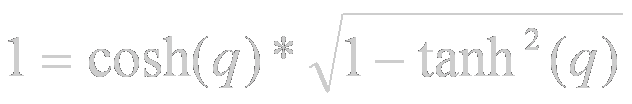
y que:
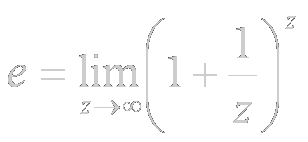
de donde resulta que:
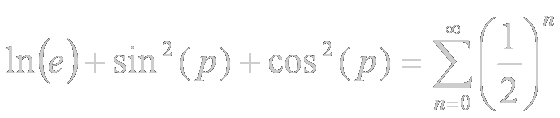
a su vez, puede ser escrita de la siguiente forma, más clara y transparente:
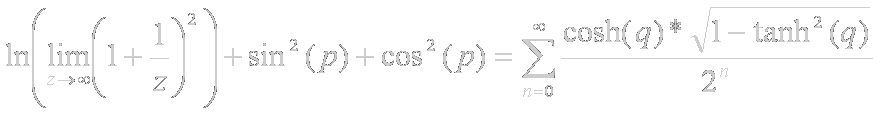
Teniendo además en cuenta que:
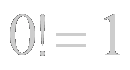
y que la matriz invertida de la matriz transpuesta es igual a la matriz transpuesta de la matriz invertida (bajo la hipótesis de un espacio unidimensional), conseguimos la siguiente simplificación (gracias al uso de la notación vectorial):
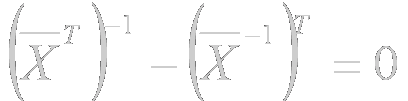
si unificamos las expresiones simplificadas:
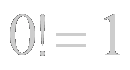
y:
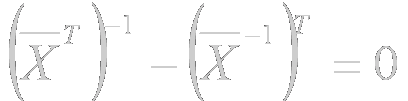
será obvio obtener:
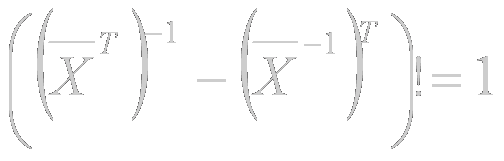
Aplicando las simplificaciones descritas anteriormente, resulta que, de la ecuación:
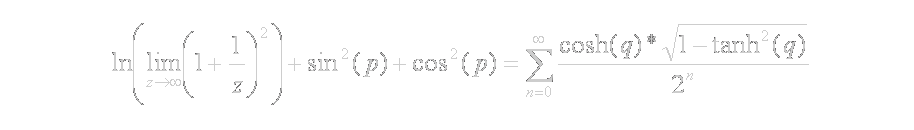
obtenemos finalmente, de forma totalmente elegante, legible, sucinta y, sobre todo, comprensible para todos, la bellísima ecuación:
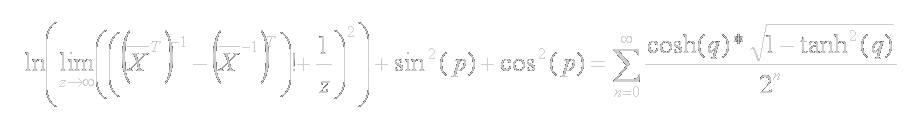
que, convengamos, es mucho más profesional que la parbulienta, vulgarísima, anodina y plebeya ecuación original:
1 + 1 = 2
Esta presentación fue confeccionada para los amigos abogados, para que sepan que también los ingenieros poseemos la suficiente capacidad para complicar las cosas y hacerla de tos... y en ¡GRANDE!
Pueden informar de ella a sus amigos ingenieros, quienes sabrán apreciar la humilde alma ingenieril que nos anima a seguir transformando al mundo.
Saludos cordiales.
Se murió un ingeniero y se fue a las puertas del Cielo.
Sabido es que los ingenieros por su honestidad siempre van al Cielo. San Pedro buscó en su archivo, pero últimamente andaba un poco desorganizado y no lo encontró en la maraña de papeles, así que le dijo:
"Lo lamento, no estás en listas...". De modo que el ingeniero se fue a la puerta del Infierno y le dieron albergue y alojamiento inmediatamente.
Poco tiempo pasó y el ingeniero se cansó de padecer las miserias del infierno, y se puso a diseñar y construir mejoras.
Con el paso del tiempo, ya tenían ISO9000, sistema de monitoreo de cenizas, aire acondicionado, inodoros con drenaje, escaleras eléctricas, equipos electrónicos, redes de telecomunicaciones, programas de mantenimiento preventivo, sistemas de control visual, sistemas de detección de incendios, termostatos digitales, etc., etc., y el "Inge" se hizo de muy buena reputación.
Un día Dios llamó al Diablo por teléfono y -con tono de sospecha-le preguntó:
"¿Y qué... cómo están por allí en el infierno?"
"¡Estamos a todo trapo! Tenemos ISO9000, sistema de monitoreo de cenizas, aire acondicionado, inodoros con drenaje, escaleras eléctricas, equipos electrónicos, Internet, etc. Oye, apúntale mi dirección de mail, es: eldiablofeliz@infierno.com... ¡Y no sé cuál será la próxima sorpresa del ingeniero!".
"¿Qué?, ¡¿QUE?! ¿Tienes un ingeniero allí? Eso es un error, nunca debió haber llegado ahí un ingeniero. Los ingenieros siempre van al cielo, eso está escrito y resuelto ya. ¡Me lo mandas inmediatamente!".
"¡Ni madre!. Me gusta tener un ingeniero en la organización... y me voy a quedar con él eternamente".
"Mándamelo o... ¡TE DEMANDARE!".
Y el Diablo, con la vista nublada por la tremenda carcajada que soltó, le contestó a Dios: "¿Ah sí?... y por curiosidad... ¿DE DONDE VAS A SACAR UN ABOGADO?".
Un hombre que vuela en globo, se percata de que está perdido, por lo que maniobra y desciende hasta que divisa a alguien en la calle, y grita:
-¡Disculpe! ¿Podría usted ayudarme?, he quedado a las dos con un amigo, llevo media hora de retraso y no sé donde me encuentro.
-Claro que sí, le contesta, se encuentra Ud. en un globo de aire caliente a unos 30m de altura, entre los 40 y 42º de latitud norte y los 58 y 60º de longitud oeste.
-Es Ud. ingeniero ¿verdad?-, dice el del globo.
-Si señor. Lo soy. ¿Cómo lo adivinó?
-Es simple. Porque todo lo que me ha dicho es "técnicamente correcto", pero "prácticamente inútil". Continúo perdido, llegaré tarde y no sé que hacer con su información...
-Es Ud. gerente, ¿verdad?-, preguntó el de la calle.
-Sí señor. ¿Cómo lo ha sabido?
-Es simple. No sabe dónde está ni a dónde va. Ha hecho una promesa que no puede cumplir y espera que otro le resuelva el problema. De hecho, se halla exactamente en la misma situación que estaba antes de encontrarnos, salvo que ahora, por alguna extraña razón... ¡la culpa es mía!
Un tipo iba caminando por la calle cuando de repente lo para un ladrón enmascarado, arma en mano, y le dice:
-¡Anda! ¡Pronto! Este es un asalto. ¡Dame tu reloj!
El tipo le da su reloj (una imitación Rolex comprada a través de un correo basura por Internet)...
El ladrón se molesta:
-¿Qué es esto? ¿Una imitación? ¡Dame tu billetera!
El hombre le da su billetera de plástico imitación de Pierre Cardin con una tarjeta de transporte público y 20 pesos.
El ladrón se enoja:
-¿¡Qué carajos es esto!?... Tu traje está todo desgastado, tu celular es pirata, tu reloj, que aparenta ser bueno, es de imitación... estás más jodido que yo. ¿A qué te dedicas?
-El tipo avergonzado, contesta casi llorando: ¡Soy ingeniero!
El ladrón emocionado, quitándose la máscara le pregunta:
-¿De verdad colega? ¿De qué generación?
Un cura, un médico y un ingeniero estaban una mañana jugando al golf.
Quizo la suerte que delante de ellos estuviera jugando otro grupo de golfistas bastante lento, por lo que siempre tenían que estar esperando.
-¿Qué pasa con estos cabrones?- se queja el ingeniero. -¡Debemos de llevar esperando 15 minutos!
-¡No sé, pero nunca he visto tanta ineptitud!- interviene el médico.
-Aquí llega Luis el jardinero- informa el cura. -Vamos a preguntarle...
-¡Hola Luis! Oye: ¿Qué pasa con ese grupo que va delante de nosotros? Son un poquito lentos, ¿no?
-¡Oh sí! Es un grupo de bomberos ciegos...- contesta el jardinero. -Perdieron la vista al intentar salvar de las llamas la sede de nuestro club el año pasado y, en compensación, les dejamos jugar siempre gratis.
El grupo se quedó callado un momento.
-¡Qué triste!- dijo el cura. -Rezaré una plegaria especial por ellos esta noche.
-Yo intentaré contactar con un colega mío, que es oftalmólogo, para ver si se puede hacer algo por ellos- añade el médico.
Y dice el ingeniero: -¿Y por qué chingados no juegan de noche?

La fórmula es el resultado de una colaboración entre Vauxhall Motors y el profesor de matemáticas Simon Blackburn, del Royal Holloway College de la University of London.
El profesor Blackburn comentó: "Estacionar el auto es algo que la mayoría de nosotros hacemos diariamente, y todos nos sentimos frustrados por ello ocasionalmente. Si entendemos los ángulos y dimensiones de nuestro auto, entonces podemos estacionarnos de una manera suave y confiada. Todos hemos tenido la experiencia de ignorar un espacio por no estar seguros de si cabemos o no. Esta fórmula resuelve ese problema".
Aplicándola a instrucciones básicas para estacionarse, se puede saber exactamente cuando torcer el volante para deslizarse en el espacio perfectamente.
(V.periódico Telegraph del 11 de diciembre de 2009).
Definición de un ingeniero químico especialista en alimentos (según el webmaster): Es aquel experto en menjurjería capaz de hacer que la mierda parezca pan y sepa como a pan.















El porqué de estudiar ingeniería y sus efectos.
- Ya no te da pena babear en clase.
- Sabes dormir con los ojos abiertos.
- El café y la Coca-Cola son herramientas, nunca caprichos.
- Escuchas el Himno Nacional 2 veces en la radio, sin levantarte de tu silla.
- Has dormido más de 20 horas seguidas en un fin de semana.
- Has cabeceado en el baño.
- Tu hermano(a) cree que es hijo(a) único(a).
- Has escuchado todos tus discos en menos de 48 horas.
- No eres visto en público sin ojeras.
- No eres visto en público sin lentes oscuros.
- Cuando recibes una invitación, va seguida de la pregunta "¿o tienes mucha tarea?".
- Pierdes las llaves de tu casa por una semana y no te das cuenta.
- Comienzas a volarte clases... comidas y cenas.
- Te has lavado los dientes y el pelo en el baño de la facultad.
- Has descubierto los beneficios de raparte o traer el pelo chiquito.
- Odias a la gente que te dice "yo iba a estudiar ingeniería en..." y te lo dicen bien a la ligera, pero no tienen idea de los problemas que te trae la carrera, o peor aún, los que nunca acabaron la carrera y creen que por eso ya son ingenieros.
- Por vez primera desde el inicio de tu pubertad dejas los lentes de contacto y usas tus fondos de botella.
- Eres un as a la hora de buscar programas en internet y/o páginas de proveedores o cualquier tipo de información para trabajos y casos de diseño.
- Haces trabajos finales que son escritos, la noche antes de la fecha límite.
- Combinas desayuno, comida y cena en UNA gran cena.
- No concibes las vacaciones como otra cosa sino como tiempo para dormir.
- Te has emborrachado junto con tus profesores.
- Constantemente creas excusas para explicar a tus profesores de materias que no son de la carrera, el por qué no hiciste la tarea.
- Alguien alguna vez te dijo "flojo" y quisiste asesinarlo.
- Tus pesadillas consisten en no terminar algo o no llegar a tiempo a algún lugar.
- Puedes vivir sin contacto humano, comida o luz solar, pero si se descompone tu computadora, o internet... ¡CAOS TOTAL!
- Puedes utilizar Excel, Matlab, Mathcad o cualquier programa para realizar cálculos y/o gráficas.
- A tus papás les da miedo usar las palabras como "¿ya terminaste?" enfrente de ti.
- Te emocionas si tus datos quedaron bonitos en la gráfica.
- Compras libros carísimos que probablemente en tu casa sólo tú entiendes.
- Estás harto de la gente que te dice "yo iba a ser ingeniero pero no me gustan las matemáticas".
- Tu archirrival natural se vuelve un profesionista: Lic. En cualquier cosa...
- No hay mejor lugar para dormir, que 2 bancas unidas y una mochila de almohada.
- Posees la marca de la modernidad: un callo en la parte baja de la palma de la mano por el uso constante del mouse.
- A tu pobre computadora ya no le caben mas programas ni más PDF's.
- Haz conseguido la habilidad de dormir en cualquier tipo de soporte ya sean teclados, mochilas, tus compañeros, el suelo, comida, etc.
- Miles de veces has estado en un amanecer, sin embargo nunca viste uno.
- Dejas de ver a otros seres humanos por meses aunque para ti sólo ha sido un día.
- Tu perro te ladra y ya no te reconoce pues haz vivido fuera de tu casa por unos días ¿o fueron semanas?
- Siempre tienes la tonta idea de que tu trabajo finalmente será reconocido.
- Para ti no hay diferencia entre el horario de verano y el normal.
- Nace tu nuevo sobrinito y dices "¿a poco mi hermana estaba embarazada?".
- Tu casa cumple la función de hotel, solo llegas a bañarte y a dormir (de vez en cuando).
- Tus amigos que estudian otra cosa no tienen el mismo concepto de TAREA que tú, siempre dicen "¡Ay! pues la haces antes de clase" o "Pues pídesela a alguien" o peor aún "Pues no la hagas".
- Odias que tus papás te digan "¡Ya duérmete!" o "Si no vas a acabar... pues ya vete a dormir" o hasta la simple pregunta "¿Te falta mucho?" puede llegar a irritarte.
Vagabundeando por el cosmos
(30 de noviembre de 2013).
This is how an engineer feels when he's surrounded by idiots
A marvelous video fully expresses the contrast between an engineer's rational mind and the others he sometimes must encounter at work for whom words are the wind that powers sales.
Guess which one's the engineer.
My engineer friend George sometimes looks at me as if I'm a rancid chicken wing in a Michelin-starred restaurant.
He doesn't understand why I don't think logically, rationally, understandably -in short, why I don't think like him.
It causes him to foam at the lips and emit high-pitched noises, not unlike those created by sheepdogs that have been run over by tractors.
I never quite grasped what his problem was until I saw a YouTube video called "The Expert".
This shows a meeting in which, quite frankly, everyone is either ridiculous or obsequious. Everyone except Anderson the engineer, of course.
The task his organization is being set is to create seven red lines.
One slight kink is that these lines must be perpendicular. Moreover, some must be drawn with green ink and some with transparent ink.
Of course, this is nonsense. But Anderson's project manager doesn't mind if it's nonsense. He says yes to everything. That's his job.
You know you're in trouble with an engineer when he says: "I'll simplify." Translation: "I'll try to get you complete dunderheads to understand why you're such complete dunderheads."
These dunderheads, however, are so dunderheadish that they won't take sense for an answer. They believe red lines can be transparent and that seven lines can all be perpendicular to each other.
Anderson tries so hard. He begins with patience. He resorts to his days at high school. Nothing works.
He gets accused of not seeing the overall picture. He gets spoken to as if it is he, in fact, who is the complete idiot.
So many businesses truly run like this. So many times co-workers or clients will come to you and call you the expert. This is shortly before they tell you they know better.
"Why are you asking me then?" you shriek inside.
That is the kind of "why" that bedeviled Socrates until the very end.
Chris Matyszczyk
(v.c|net news del 1o.de abril de 2014).
¿Cómo tomamos las decisiones más importantes de nuestras vidas? Probablemente mal, intentando que nadie salga perjudicado y adoptando una actitud pasiva frente a las opciones que disponemos. Sin embargo, existen principios que nos pueden ayudar a conseguir la mejor opción posible no sólo para nosotros, sino también para los demás. Se trata de darle la vuelta a la tortilla e intentar que ninguna decisión sea salomónica: si las 2 mujeres hubiesen aceptado partir al hijo por la mitad, ninguna de ellas habría podido disfrutar verdaderamente de él.
Este principio, llamado el "problema del matrimonio estable" ha sido descrito por la matemática del Centro UCL para el Análisis Espacial Avanzado Hannah Fry en su libro The Mathematic of Love (TED Books) y fue enunciado por 1a. vez en 1962 por David Gale y Lloyd Shapley. Aunque es semejante, no tiene nada que ver con la ecuación de la "teoría de la decisión" que nos permite saber cuánto tenemos que buscar para encontrar a nuestra pareja ideal. Según la lógica que expone Fry, lo importante no es tanto el cálculo probabilístico como el orden de preferencias entre los participantes en la elección y quién tiene la iniciativa en un momento de elección.
El problema de la mejor opción
El planteamiento de la cuestión es el siguiente: tenemos 2 grupos de elementos del mismo tamaño que deben unirse entre sí, como puede ser, por ejemplo, 3 chicos y 3 chicas en un bar nocturno. Cada uno de ellos tiene una idea clara de cuál es su opción preferida, pero claro, dependen de la voluntad de sus amigos y de las personas del sexo contrario. El objetivo debería ser formar parejas sean estables, es decir, que prefieran estar juntas que por separado. ¿Hay alguna forma posible de hacerlo?
La solución fue proporcionada por Gale y Shapley a comienzos de los años 60 en un artículo publicado en The American Mathematical Monthly. Según explicaron, siempre es posible, a través del algoritmo O (n²), donde "n" es el número de hombres y mujeres. Dicho de otra forma, este proceso consistiría en que todos los hombres eligiesen en un 1er. lugar reunirse con la mujer a la que prefieren (o viceversa, obviamente). Algunas tendrán su cita, otras no, pero no deben desesperar. Aquellas que sí han tenido un encuentro rechazan a los que no les gustan, pero las que se han quedado interesadas por su cita se lo apuntan y quedan transitoriamente emparejados con ellos... pero no toman ninguna decisión definitiva.
En la siguiente ronda, los hombres que no tienen pareja se proponen a la siguiente de su lista, sea esta cual sea, y el proceso vuelve a ocurrir: las mujeres rechazan a los que no les gustan y dicen "quizá" a aquellos que les gustan más que ninguna otra opción. Es posible que, en dicho caso, las mujeres conozcan a alguien que prefieren a su anterior elección. El proceso se repite hasta que cada mujer se queda sólo con un candidato. El resultado es que cada mujer y cada hombre terminarán emparejados con la mejor opción posible, teniendo en cuenta que no se puede forzar al resto a cambiar sus gustos.
Se trata de una solución estable, pero no óptima. En realidad, hay 3 escenarios posibles al aplicar este algoritmo: que los hombres obtengan sus primeras elecciones y las mujeres, sus terceras; que todo el mundo consiga su segunda opción; y que las mujeres obtengan su primera opción y los hombres la tercera. Aunque parezca una solución injusta, en realidad es más bien un café para todos. Se considera estable puesto que la inestabilidad aparece cuando ambos miembros de la pareja preferirían una alternativa. Sin embargo, esta asimetría nos dice mucho de cómo deberíamos tomar elecciones.
El que golpea primero, golpea dos veces
Una posible conclusión de este experimento es que no debemos quedarnos con los candidatos a la primera en el caso de que sean ellos quienes se presenten, puesto que probablemente habrá una mejor opción que surgirá más tarde. Pero lo más importante es que, tal y como está planteado el problema, los hombres conseguirán la mejor opción posible, mientras que la mujer tendrá que quedarse con la menos mala. La conclusión, explica Fry, es que "la persona que pregunta (y está dispuesto a enfrentarse al rechazo hasta conseguir la mejor opción) sale ganando". Por el contrario, los que esperan a ver las opciones, como las mujeres, tienen que quedarse con la opción menos mala.
Esto puede ser aplicado a otros ámbitos, y de hecho se aplica. Si un responsable de recursos humanos intenta buscar el mejor candidato, es preferible que sea él quien acuda directamente a sus preferencias (aunque pueda ser rechazado por estas) que esperar a ser la empresa elegida entre una lista de competidores. Si buscamos trabajo y tenemos una preferencia clara de dónde queremos que nos contraten, y nos ofrecemos a las opciones mejor valoradas, terminaremos fichando por la organización disponible que más nos gusta. En resumen, tener la iniciativa nos ayuda a encontrar antes la mejor opción.
Este mismo principio se aplica en otros sistemas, como el de la adjudicación de médicos a determinados hospitales en Estados Unidos. En un pasado, los hospitales acudían a los médicos que preferían, que elegían la opción menos mala, pero que los hacía infelices. Este sistema fue dado la vuelta para que fuesen los médicos quienes seleccionasen el centro en el que preferían trabajar. Alvin Roth y Lloyd Shapley obtuvieron el Premio Nobel de Economía en el año 2012 precisamente por el perfeccionamiento de este algoritmo, que tomó forma en "la teoría de las asignaciones estables y la práctica del diseño de mercado".
Héctor G.Barnés
(v.El Confidencial del 8 de julio de 2015).



Los aspectos técnicos de la construcción del muro son más complicados que los financieros. Un ingeniero experto en estructuras, Ali F. Rhuzkan se tomó la molestia de hacer los cálculos y cree que es casi imposible. "El señor Trump es experto en hacer edificios grandes. No tiene idea de que un muro de 1,954 millas es varias veces más complicado que un edificio de 95 pisos...", dice Rhuzkan.
Para ser un muro y no una valla, como ha dicho Trump, debe estar hecha de un material que no sea poroso, por ejemplo concreto. Para evitar que le hagan túneles por abajo, debe tener cimientos de metro y medio. Para que no la brinquen por arriba, debe ser de alrededor de 6 metros de altura. "Se trataría de una de las obras de ingeniería más importantes en la historia de la humanidad... sólo hay algo comparable: la muralla china", dice Rhuzkan.
Este ingeniero usa como referencia "cercana" una obra clave en la historia de la ingeniería de Estados Unidos, la Presa Hoover, que sirve para dotar de agua para irrigación y uso urbano a Nevada y California, además de producción de energía eléctrica.
El muro requeriría 3 veces más material que la Presa Hoover. Esto es 12.6 millones de yardas cúbicas de concreto y 10.1 millones de pies cúbicos de acero. El principal reto es cómo producir e instalar la muralla, dice Rhukzan. Las altas temperaturas de la zona fronteriza hacen imposible que el concreto sea colado en el lugar donde se instalará. El muro deberá estar hecho de piezas prefabricadas que serían transportadas por territorios donde no siempre hay caminos.
La Presa Hoover fue construida por 20,000 trabajadores, de los cuales murieron 112. El muro de Trump podría necesitar un número similar, quizá mayor. ¿Cuántos estadounidenses estarán dispuesto a trabajar a 40 grados centígrados? ¿Se atreverá Trump a contratar mexicanos?
Este es el vínculo al análisis del ingeniero Rhuzkan http://www.nationalmemo.com/an-engineer-explains-why-trumps-wall-is-so-implausible/
Luis Miguel González
(v.pág.9-A del periódico El Informador del 14 de enero de 2017).


Considérese esta pléyade de estrellas que brillaron -varias- en el nivel nacional y por lo menos uno es un hito de la arquitectura en el nivel mundial.
¿Qué tienen en común las siguientes gentes? Luis Barragán, Pedro Castellanos, Rafael Urzúa, Juan Palomar y Arias, Ignacio Díaz Morales, Julio de la Peña, Jorge Matute, Miguel Aldana, Yves Palomar y Loriot de la Salle, Hermann y Carlos Petersen Biester, Javier Vallejo, Guillermo Blanco, Guillermo González Luna, Luis Ugarte, Gabriel Ugarte, Hugo Romo, el Padre Uribe, Jorge G de Quevedo...
Que todos fueron ingenieros civiles (buenos ingenieros civiles). No nomás de título: todos hacían las cosas como las haría un ranchero. El acercamiento de los ingenieros a la arquitectura difiere radicalmente del de los arquitectos. Los ingenieros van a lo que van, evitando complicaciones y florituras. Casi nunca se cae lo que construyen. Hay lógica, sentido común, serenidad, gravitas. Sus materiales son dignos y severos, y la expresión final de la edificación refleja todo esto y algo más: una potente poesía derivada de la austeridad a veces casi franciscana de sus hechuras. Hay un vuelo.
Todo lo contrario con tantos arquitectos. Fachas, materialitos brillosos o piedrín (¡resucitó el piedrín!), columnas chuecas, chipotes, puterías variadas, alardes estructurales costosos, ventanas carísimas a las que se les mete el agua, oscura terminología, "conceptos" hechos bolas y un largo etcétera. Que quede claro que existen muy buenos arquitectos... cuando piensan como ingenieros.
Axel Arañó tiene una interesante teoría para cerrar las frecuentemente dañinas escuelas de arquitectura: 4 años de ingeniería, 4 de filosofía y 4 de práctica profesional con un arquitecto decente. (Las cifras son de memoria). Y listo. Menos agresiones urbanas, menos pretensión, menos bienalitas en las que ciertos arquitectos aplauden y se soban el lomo con otros. Menos revistas mainstream, menos congresos balines, menos starchitects de petatito. Más viajes al campo, más comprensión de cómo proyecta y construye la gente que no tiene dinero, más conocimiento de sistemas de construcción milenarios que funcionan perfectamente, más familiaridad con árboles y plantas, con el paisaje todo. Puede ser una alternativa que tanto nos urge.
Si se toma la molestia (¡vamos, no es tan duro!) de recorrer a pie o en bicicleta múltiples contextos de Guadalajara se podrá advertir un extraordinario fenómeno: de 1926 a 1955 la arquitectura tapatía vivió una edad de oro. El fenómeno fracasó, casualmente, cuando los primeros egresados de la Escuela de Arquitectura ¡de Díaz Morales! comenzaron a actuar profesionalmente. Fue, en tantos casos, un desastre.
Aprendamos la lección. ¿Cómo lo haría un ranchero? ¿Cómo lo haría un (buen) ingeniero? Pues así. Sin complejos.
Juan Palomar Verea
(v.pág.10-A del periódico El Informador del 13 de noviembre de 2019).

(V.I am an IT expert, but not geek del 23 de marzo de 2020).


Vínculos interesantes
What is Mathematics?
 Regreso a mi página base
Regreso a mi página base
El Tesoro de la Jumentud > La Página de las narraciones interesantes > Una de ingenieros
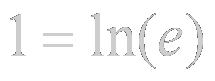
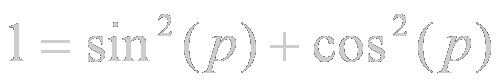
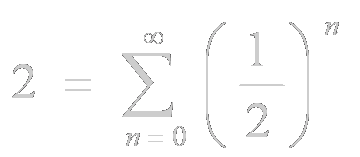
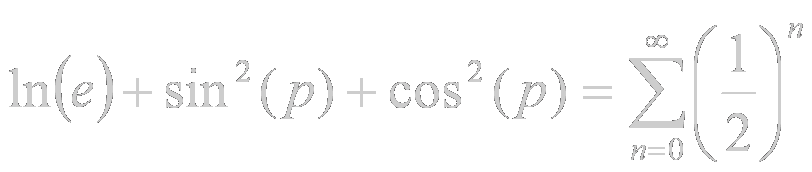
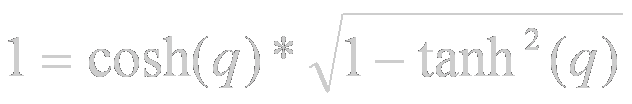
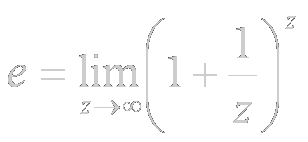
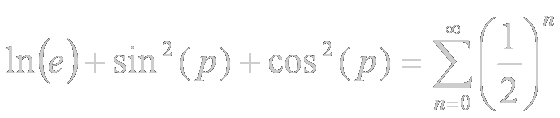
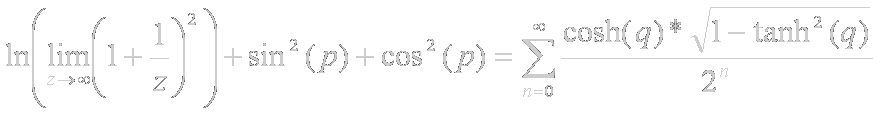
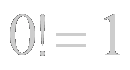
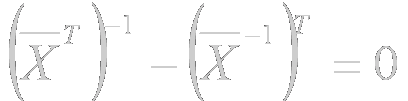
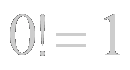
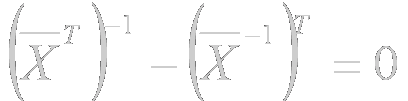
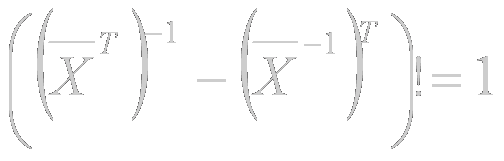
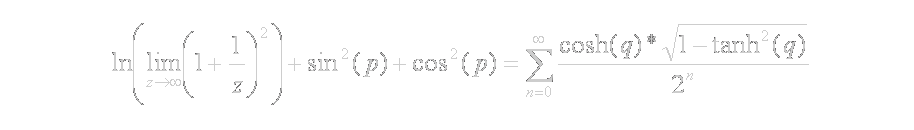
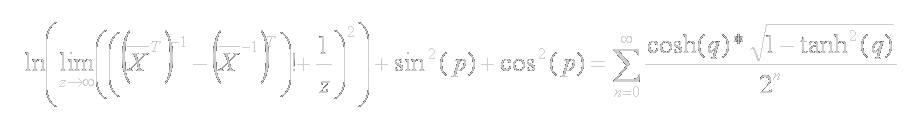
























 Regreso a mi página base
Regreso a mi página base